
Critérios de semelhança de triângulos
///////////////////////////////////////////////////////////////////////////////
{ 1 }
Critério LLL de semelhança de triângulos
Dois triângulos são semelhantes quando os comprimentos dos lados de um são diretamente proporcionais aos comprimentos dos lados correspondentes do outro.

{ 2 }
Critério LAL de semelhança de triângulos

Dois triângulos são semelhantes quando os comprimentos de dois lados de um são diretamente proporcionais aos comprimentos de dois dos lados do outro e os ângulos por eles formados em cada triângulo são iguais.
{ 3 }
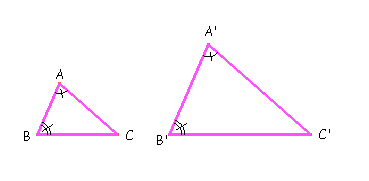
Critério AA de semelhança de triângulos
Dois triângulos são semelhantes quando dois ângulos internos de um triângulo são iguais a dois ângulos internos do outro.
-
BÂC = B'Â'C'
-
B = B'
Sites que consultamos para compreender a matéria
{ 4 }
{ 5 }
Exercícios

prova que os triângulos [ABC] e [ADE] são semelhantes


Resolução:

Resolução:
Os triângulos são semelhantes pois se aplicarmos o critério LLL verificamos que os lados são proporcionais, ( r = 2,5 ).

Resolução:
Os triângulos são semelhantes, pois se aplicarmos o critério LAL verificamos que dois dos lados do triângulo são proporcionais (r = 2 ) e o ângulo por eles formado é igual.

Resolução:
Os triângulos são semelhantes porque se aplicarmos o critério AA verificamos que dois dos ângulos de cada triângulo são iguais, o ângulo restante também, é igual porque a soma de todos os ângulos internos de um triângulo é 180º e 180 - 40 - 70 = 70º que seria a amplitude do ângulo restante em ambos os triângulos.



